Copyright© 2007  Попов В.П.  Организация. Тектология XXI. All Rights reserved

 

5. Порядок и хаос в организациях

5.1. Хаос, порядок, сложность

Прежде чем начать дискуссию по теме настоящей главы, следует определиться в смысле терминов. Что есть хаос? И что такое порядок? Как эти понятия относятся к элементам и связям организаций? Неясным остаётся также понятие «сложность».

«В мифах Древней Греции и в учениях античных мудрецов хаос рассматривается не просто как безликая бездна, бесформенное первоначало всех мирских творений, а как универсальный творческий принцип, потенциально, в свернутом виде содержащий в себе все образцы (формы) становления. Хаос все раскрывает и все развертывает, всему дает возможность выйти наружу, но в то же самое время он все поглощает, нивелирует, прячет вовнутрь» [105]. Можно отметить, что субъективная оценка хаоса, выраженная на современном языке, звучит как нечто непознаваемое, непонятное, безликое, бесформенное. Хаотические явления ассоциируются со случайностью, непредсказуемостью. Налицо противоречие. Хаос есть бесформенное состояние, но из него появляется много оформленных вещей.

Это противоречие может быть разрешено, если в нем выделить объективную и субъективную составляющие. В очень темной комнате ничего не видно, но из этого не следует, что там пусто. Когда из такой комнаты выбегает чёрная кошка, это не означает, что она возникла из темноты. Очень сложная структура не воспринимается сознанием (не моделируется силами мозга). Противоречие разрешается следующим образом. Недоступный для познания порядок в сознании ощущается как хаос. Слишком большая сложность – это тьма для сознания.

По мере развития методик и углубления исследований в хаосе можно увидеть очень сложную, не сразу постигаемую умом структуру. Например, Э. Лоренц в 1963 г. описал дифференциальными уравнениями структуру глобальных метеорологических явлений, которые ранее считались хаотическими. Известная функция распределения молекул по скоростям, выведенная Максвеллом [168], свидетельствует, что движения молекул газа не представляют собой полный хаос, а имеется определенный порядок в распределении молекул по скоростям движения. При определённой температуре можно рассчитать, сколько будет молекул «холодных», сколько «горячих» и сколько «тёплых». Несмотря на свободу «воли» передвижения, молекулы в газе строго ранжированы по кинетическим энергиям. Это ли не пример структуры хаоса, но увидеть её можно только с помощью специальных экспериментов. По мере того, как сознание находит способы моделирования очень сложных, запутанных ситуаций, в хаосе обнаруживается некоторая упорядоченность

Теория вероятности описывает широкий круг явлений, где фигурируют случайности. Например, бросание игральной «кости» (кубик, грани которого помечены числами). Точно предсказать появление желаемого числа невозможно, но можно предсказать частоту появления этого события. При многократных бросках вероятность появления числа составит 1/6. Чем больше число бросков, тем точнее выявляется вероятность 1/6. Очевидно, явления связанные с понятием вероятность, не самые хаотичные. Они обладают инвариантом, т. е. устойчивостью частот. Теория вероятности выявляет в событиях некоторую закономерность.

Однако при экспериментировании с кубиком не замечают самое вероятное событие - факт его падания на стол. Если не произойдет падения, то обсуждать «на какую сторону упадёт кубик» не имеет смысла. Как видно на фоне случайных событий всегда можно обнаружить детерминированные.

Бифуркации часто приводятся как пример случайного развития. Но такая случайность все же предполагает существование детерминированного поля возможностей. Шар, находящийся на вершине пирамиды, может скатиться в любую из четырех сторон, но не взлететь вверх. Это пример бифуркации по схеме «или – или». Возможностей всего четыре, но не больше.

В биологии долго господствовала парадигма случайности мутаций. Но, что есть случайность, умалчивалось. Если число испытаний конечное, можно подсчитать частоту заданного события, которая не всегда носит вероятностный характер. Одни мутации происходят с определенной частотой, третьи фиксируются редко, другие – с переменой частотой (мода на мутации), четвертые – никогда.

Случайность и вероятность - это не одно и то же. Случайность имеет форму или гауссовского, или гиперболического распределения. В гиперболическом распределении нет средних величин, и точность измерения нельзя повысит количеством измерений, т.е. нет гауссовской дисперсии. Но инвариантом является устойчивое распределение частот [225].

Иногда с хаосом отождествляют диссипативные процессы, которые не всегда является хаосом, они могут осуществляться по организованным каналам, например, выделение отходов в живых организмах, организация вывоза отходов на свалку, связи между подсистемами организации и т.п.

Если диффузия осуществляется в абсолютно однородной среде, то она вполне предсказуемым образом распространяется, как раздувающаяся сфера. Диффузия тепла вдоль металлического стержня закономерно распространяется вдоль стержня.

В работе И. Пригожина «Порядок из хаоса» не даётся чёткого определения, что есть порядок и что есть хаос [183]. Например, ламинарный поток жидкости Пригожин И. определяет, как хаос, ибо невозможно описать движение каждой отдельной молекулы. Когда же при увеличении скорости потока самопроизвольно возникают турбулентные вихри, он оценивает это событие, как упорядоченность в ходе самоорганизации.

Другим часто цитируемым примером возникновения порядка из хаоса являются опыты Бернара. При нагреве тонкого слоя масла хаотическое конвективное движение переходит в упорядоченное, возникают потоки в форме правильных шестигранников (ячейки Бернара).

Вычислительные эксперименты открыли процессы самопроизвольного возникновения структур горения с множеством максимумов. Через определенное время, возникшие структуры, распадались. Диссипация аттракторов проходила не случайным образом, а по определенным каналам, т.е. диссипативные процессы могут быть структурированными [105].

В ламинарном потоке траектории движения каждой молекулы человеческий ум отследить не может, избыток информации воспринимается как хаос.

Появление крупных завихрений на фоне хаотической составляющей ощущается как порядок [183]. Аналогичные идеи высказывал Д. Бом. «Я бы сказал, что не существует беспорядка, но этот хаос - это порядок бесконечно сложной природы». Получается, что порядок есть ограниченное, поэтому умопостигаемое количество информации. Рассмотрим примеры.

На антенну радиоприемника поступают сигналы от сотен радиостанций. В результате наложения радиоволн получается информационный шум (хаос). Резонансный фильтр приемника способен выделить из шума полезную радиопередачу. Перестраивая приемник, можно услышать много полезных радиопередач. Получается, что хаос - это сумма полезной информации, не воспринимаемая в совокупности. Когда в беспорядочных процессах удаётся увидеть нечто простое, понятное сознанию, то ощущается рождение порядка.

Хаос не может быть статичным, т.к. статика человеком воспринимается легко. Есть время её исследовать и осмыслить. Хаос динамичен. Если структура существует кратковременно, и её не успевают заметить и изучить, то такие объекты не воспринимаются сознанием. Шаровая молния ускользает от научного исследования, т.к. непредсказуемо появляется в неожиданном месте. Аналогичная картина складывается с НЛО. Вакуум долго казался пустотой потому, что из него на мгновение появлялись и исчезали частицы прежде, чем сознание с помощью аппаратуры успевало их зафиксировать [108]. Позже осознали, что вакуум имеет структуру.

Другим примером преодоления динамичного хаоса является прогноз погоды на ближайшие сутки. По причине недостаточного быстродействия ЭВМ не успевала произвести необходимые расчеты.

В силу того, что Мир устроен очень сложным образом для человеческого понимания, а скорость познания ограничена дефицитом энергии, вещества и времени, абсолютное знание никогда не будет достигнуто, поэтому хаос (непознанное) останется вечным спутником человека. Несмотря на то, что область знаний постоянно расширяется, открываются новые горизонты незнания (хаоса). Во многих случаях люди и не стремятся уточнять модели, т.к. допустимые ошибки не мешают существованию и развитию человечества. «Плоскую» геометрию Эвклида, несмотря на неточности, изучают во всех школах потому, что она проста. Но более точные и сложные геометрии Лобачевского и Римана знают лишь единицы. Сложные модели остаются недоступными для понимания большинства людей в силу особенностей их интеллекта. Однако в тех случаях, когда упрощённые модели природных явлений не адекватны потребностям человечества, возникает необходимость уменьшать в них долю хаоса.

Но существует ли онтология хаоса вне субъекта наблюдения, или все проблемы ограничиваются гносеологией? Рассмотрим примеры.

Причиной случайностей могут быть непонятые закономерности (Дарвин), неустойчивое движение (игральные кости), недостаточность знания, скрещение несогласованных путей движения, предпочтительный выбор [225].

Если изучается система с очень большим количеством элементов, которые отличаются друг от друга свойствами или поведением, индивидуальное описание каждого элемента практически невыполнимо по «техническим» причинам. Как нет возможности описать каждую отдельную молекулу в жидкости или газе, также невозможно описать каждую песчинку на пляже, каждый кристаллит в горных породах, каждую рыбу в стае, каждую клетку в колонии бактерий и т.п. Для полного описания не хватит ресурса времени и информационной ёмкости всех ЭВМ.

Такие объекты можно было бы отнести к онтологии хаоса, если бы не существовали методы математической статистики, функции распределения (Гаусса, Максвелла и др.), способы усреднения параметров. Давно открыты «газовые законы», позволяющие с высокой точностью предсказывать поведение «хаотических» газов. Для описания газов и жидкостей используют термодинамические параметры «температура», «давление», «объем» (PV=nRT), которые являются функциями средних кинетических энергий молекул. Давление газа на стенки сосуда является следствием стохастических движений молекул, поэтому давление пульсирует, совершает флюктуации. Если поведение газа можно предсказывать, моделировать, то хаотическим его назвать нельзя.

Разновидностью случайного события является предпочтительный выбор. Известная задача с Буридановым ослом не имеет логического решения потому, что логика не учитывает решений, основанных на предпочтении. Осел, находясь между двумя совершенно одинаковыми копнами сена и на равном расстоянии от них, выберет не логичный, а предпочтительный вариант. Пойдет к той копне, которая ему больше нравится.

Человеческие поступки обычно ограничены нормами нравственности, морали, религиозными убеждениями, законом. Поведение стайных животных также регулируется инстинктами, обучением, вожаком. Если известны предпочтения лидера и желание людей идти за ним, то можно предвидеть траекторию движение всего общества. Предсказания Нострадамуса, вероятно, основаны на интуитивном знании предпочтений людей.

Предпочтения можно увидеть не только в живых системах, но и в молекулярных. Химические взаимодействия межу молекулами протекают не случайно. Только для совершенно одинаковых элементов безразлично с кем и как соединяться. Предпочтительные взаимодействия являются следствием гетерогенности элементов и связей организаций. Положительный заряд притягивается только к отрицательному. Ключ подходит только к одному замку.

Понятие «бифуркация» часто иллюстрируется примером человека на распутье. Однако выбор дальнейшего пути определяется предпочтением. Даже когда все дороги кажутся одинаковыми, поворот направо или налево зависит от асимметрии человеческого тела, от предыдущих навыков, от системной памяти. Решения, принимаемые разными людьми, ввиду разных предпочтений, могут казаться стороннему наблюдателю случайными. Для конкретного человека его собственный выбор не случаен, а определяется наличием памяти (опыта). В главе 3.4 мы рассматривали роль системной памяти в выборе коридоров эволюции. Если наблюдатель знает предпочтения конкретного человека, то может предсказать его действия. Этот принцип используется менеджерами в управлении персоналом.

Другим примером является разброс попаданий при стрельбе. Механики рассчитали траекторию движения артиллерийского снаряда (парабола). Но с момента выстрела взаимодействие субъекта и объекта нарушается, и начинают действовать бесконтрольные факторы. Промах является следствием расхождения теоретических ожиданий и практических результатов.

Причиной непредсказуемости результатов стрельбы и бросания кости является потеря взаимодействия субъекта и объекта. Аналогией может служить движение автомобиля с заснувшим водителем. Но если с интервалом в доли секунды регистрировать координаты и вектор скорости летящей кости, то её положение в следующую секунду можно предсказать с достаточной точностью. Если результат события предсказуем, то, следовательно, существует определённый порядок. Однако при этом не всегда можно повлиять на результат (например, на погоду).

При стрельбе управляемыми снарядами траектория движения отслеживается, корректируется, и попадание в цель гарантируется. Таким образом, хаос (непредсказуемость) устраняется в результате контроля за параметрами движения.

Следует отметить, что управление любыми объектами основано на знании его поведения. Контроль и коррекция состояния осуществляется через некоторые интервалы времени. Чем устойчивее объект, тем реже вмешательство и корректировка. 

В главе 3 сформулировано понятие «виртуальная связь». Такие связи  детерминируют движение организации в определённом коридоре, как автопилот исключает хаотический полёт авиалайнера.

В математике известно понятие «странный аттрактор» - некоторая зона притяжения, каких – либо процессов, описываемая нелинейными дифференциальными уравнениями. Траектории фазовых состояний около странного аттрактора не повторяются, но это не основание считать его хаосом. Состояние системы в заданный момент времени можно, например, предсказать путём численных экспериментов на ЭВМ.

Итак, нам не удалось обнаружить объективного хаоса. Изыскания ума снижают неопределённость. В мысленных моделях растёт доля порядка, но никогда не достигает максимума. Всё это даёт основание предполагать, что в основе устройства Вселенной объективно лежит сверхсложный, непознаваемый порядок. Философы называют его небытием. Идеи сложности прасреды высказывалась Лейбницем (монады), Анаксимандром (апейрон). Не отказались от неё и современные исследователи [105]. «Во-первых, небытие, или прасреда, представляет собой вневременную свертку всех будущих и всех бывших формообразований мира. Но в небытии все это содержится в невыявленной форме. Природа строит на своем теле то, что соответствует её внутренним тенденциям самоорганизации. Мы «обречены» на такое настоящее, ибо оно определено прошлым и строится в соответствии с проектами будущего» (Хайддегер) [105]. Эти высказывания не противоречат той модели хаоса, которая приведена выше и свидетельствует о скрытом порядке хаоса. Проблема хаоса, скорее всего, является гносеологической.

Восприятие упорядоченности системы зависит от её агрегатного состояния и возможностей сознания. Если структура объекта проста, легко познаваема, предсказуема, то её называют упорядоченной. Атомы, объединившиеся в молекулу, теряют возможность перемещаться индивидуально, поэтому схемы строения молекул понятны даже школьникам. Но трехмерная структура белковой молекулы понятна только специалистам, хотя её упорядоченность не вызывает сомнения.

Отдельная молекула в сильно разреженном газе может двигаться в любом направлении и на любые расстояния. При попадании в гущу других молекул её возможности поведения резко сокращаются. Соседи начинают мешать, ограничивать свободу перемещения. При конденсации многие формы движения молекул вырождаются. В жидкой воде молекулы совершают движения около некоторого аттрактора. Рентгеновские исследования показывают существование ближнего порядка на фоне произвольного движения молекул. Спектры колебания молекул в жидкостях всегда более разнообразны, чем в твердых телах, т.к. молекулы жидкостей менее ограничены в своём поведении.

В монокристаллах атомы колеблются в зоне аттракторов, центром которых являются узлы кристаллической решётки. Часть времени атом располагается вблизи узла кристаллической решетки (порядок), а часть времени «гуляет» в её окрестностях (хаос). Разделить хаотическое и упорядоченное состояние атома можно только средствами сознания для удобства моделирования.

Движение клеток в колонии микроорганизмов разнообразнее, чем в составе организма. Человек на предприятии не может делать, то что хочет, а должен делать то, что нужно. Специализация отсекает лишние функции, сокращается спектр возможностей, модель поведения становится более понятной (упорядоченной). Поведение животных в стае менее разнообразно, чем за её пределами. По Фрейду поведение толпы более предсказуемо, чем поведение индивидуума.

Итак, различение порядка, беспорядка и хаоса является проблемой гносеологии. Для нас важен вывод, что порядок и хаос есть системное единство, как свет не отделим от тьмы. Отсутствие фотонов – тьма. Присутствие фотонов – свет разной интенсивности. Хаосом называется непознанный порядок. Появление познаваемых структур оценивается как упорядочение.

Однако в гетерогенных, многофазных системах, зоны разной упорядоченности могут быть соседями. К гетерогенным системам относятся горные породы, композиции полимеров, керамика, сталь, сплавы, многослойные конструкции, организмы, клетки, социумы, биосфера, космические объекты. Например, кристаллический лёд (вода) может находиться в смеси с жидкой водой (двухфазная система). В этом случае раздельность хаоса и порядка является объективной. Хаотическая и упорядоченная фазы воды сосуществуют рядом.

Следует обратить внимание, что сложный, по нашим понятиям, человеческий организм содержит фазы разной упорядоченности: газы, жидкости, аморфные и кристаллические ткани. Взаимодействие между подсистемами организаций может быть и упорядоченным (иерархия), и хаотическим (анархия). Все сложные организации в качестве системной памяти включают в себя хаотические и организованные процессы и структуры.

В контексте сказанного рассмотрим понятие «сложность». «Хаотическое» всегда относится к сложному. Слабопредсказуемые в своём поведении системы квалифицируются как сложные (см. главу 2). Таким образом, «сложность» является понятием субъективным. То, что кажется сложным для большинства людей, интеллектуал может считать понятным и упорядоченным.

Систему химических элементов упорядочил Менделеев Д.И. После упорядочения атомарного уровня, учёные стали выстраивать молекулярный, клеточный, организменный и другие уровни, которые оценивались как более сложные. Посредством аналогии покажем, что их сложность субъективная.

Допустим, кирпичи из хаотической кучи укладываются в стены дома (порядок). Разнообразие положений кирпичей в куче выше, чем в стене. Описать состояние кирпичей в куче значительно сложнее, чем в стенах дома, следовательно, куча устроена сложнее, чем стена. Парадокс, но упорядоченный дом устроен проще, чем хаотическая куча.

Чтобы получить упорядоченную скульптуру, от глыбы мрамора отсекают лишнее. Чтобы воспринять радиопередачу, отфильтровывают лишнюю информацию. Люди на предприятиях утрачивают многие свои функции в силу специализации производственных процессов. Многие действия отдаются специалистам (снабжение, бухгалтерия, маркетинг). Действия отдельных людей становятся проще, но надёжнее. Изложенную парадигму можно пояснить аналогией представленной на рис.5.1.

 

 

 

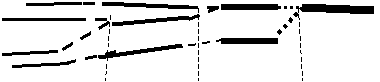
                                                                    Канат

 

Волокна                Нити                Шнуры

Рис. 5.1. Формирование уровней сложности.

Из шерстяных волокон можно сучить нить. Из нитей плести шнуры. Из шнуров - веревки (канаты). В каждой очередной скрутке возникают поперечные связи, поэтому шнур приобретает новые свойства. Описать свойства каждого отдельного волокна в клубке практически невозможно. Но описание свойств шнура (каната) не представляется проблемой. Очевидно, процесс «плетения», как и эволюция, создаёт более простую для описания систему.

Аналогичная мысль изложена в работе [105]. «Сложная система сама себя стабилизирует. Она идет в процессе развития к некоторому почти однородному состоянию, к единству и гармонии объединяющихся в ней частей, как, собственно, и полагали восточные мудрецы.… При очень сильной нелинейности вообще отсутствует спектр аттракторов, сложность вымирает. Сложная система в процессе своего развития как бы строит новую непрерывную среду, в которой колебания весьма невелики по отношению к некоему среднему состоянию, стабильно растущему в режиме с обострением».

Итак, логично предположить, что развитие идёт от сверхсложного порядка (хаос) к более простому порядку (организация). Но почему бытует устойчивое мнение, что эволюция, развитие – это усложнение? Попытаемся разобраться в сложившейся гносеологической ситуации.

В главе 4 мы пытались теоретически представить модели первобытного субстрата, который имеет сетевую структуру. Поскольку эти модели экспериментально не подтверждены, их можно относить к хаосу. Элементарные связи представлены «волокнами». Упорядоченные вещи возникают при агрегировании движущихся волокон.

Эволюция развивается в направлении сокращения количества «первобытных» элементов и связей, «свертывания» (комбинирования) их в новые агрегаты и связи. Каждая новая связь образуется из множества «старых», поэтому, если оценивать сложность по количеству первобытных связей в агрегате, то эволюция есть упрощение, развитие идёт от сложного порядка (хаоса) к простому порядку.

На рис. 5.2 графически изображена эволюционная динамика изменения количества связей в организациях. Пунктирные кривые в заштрихованной области относятся к организациям, которые воспринимаются сознанием как хаос.

Количество первобытных связей (кривая 1) постоянно уменьшается, т.к. они расходуются на появления новых структур. Однако их первичное количество настолько велико, что для науки они до сих пор представляются хаосом (темное вещество, вакуумные структуры, сетчатый мировой субстрат).

Кривая 2 отражает рост количества вновь образованных связей в новых организациях. Простые (понятные) организации с малым количеством новых связей сознание относит к упорядоченным. В ходе эволюции количество новых связей и элементов растёт. Возрастающее количество новой информации воспринимается как рост сложности. Этим объясняется парадигма увеличения сложности в ходе развития. Поэтому сплошная кривая 2 переходит в пунктирную.

 

 

           1            ХАОС

 

 

 

 

            2                                   ПОРЯДОК

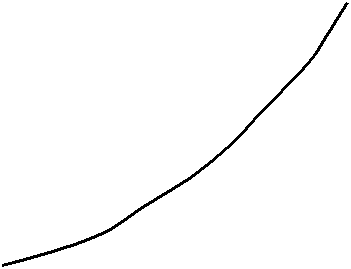                                 Э В О Л Ю Ц И Я.

Рис. 5.2. Эволюционная динамика объективного изменения количества связей в организациях. 1. – уменьшение количества  первобытных связей. 2. – возрастание количества  вторичных, агрегатных связей.

 

Сказанное можно пояснить следующим примером. Вода в целом имеет хаотическое и сложное строение, но, когда при охлаждении из неё образуется кристаллик льда, сознание ощущает появление упорядоченной структуры. При дальнейшем охлаждении образуется множество кристалликов разного размера и формы, описание этого агрегата снова вызывает ощущение сложности (хаоса). От ощущения первобытного хаоса мы приходим к ощущению вторичного хаоса, непознаваемой упорядоченности.

Если рассматривать процесс эволюции с учётом причинно – следственных связей, то следует обратить внимание на то, что для образования новых связи потребовалось множество первобытных, субстратных связей. Аналогично для изготовления одного кирпича требуются миллионы пылинок глины. А для изготовления одного дома – десятки тысяч кирпичей. Миллионы пылинок исследовать сложнее, чем изучить свойств одного кирпича. Кирпич проще (понятнее), чем килограмм глины. Итак, Мир развивается от сложного порядка к более простым агрегатам, вероятно, это является одной из причин наблюдаемого тренда эволюции. Очевидно, хаос относится к гносеологическим проблемам.

 

5.2. Энтропия

Завершение темы о природе хаоса невозможно без упоминания об энтропии (меры хаоса). Впервые понятие «энтропия» эмпирически было выведено Клаузисом в 1865 г. Эта функция вида S=Q/T (Q - теплота, Т- температура) трактуется как часть внутренней энергии системы, которая не может быть переведена в работу. Л. Больцман (1872 г.) для идеального газа теоретически вывел выражение энтропии S = K ln W, где К – константа; W – термодинамическая вероятность (количество перестановок молекул газа, не влияющее на макро состояние системы) [119]. Для многих гуманитариев приведенные формулы ни о чем не говорят. Они обращают внимание только на выводы, в которых энтропия Больцмана трактуется как мера беспорядка, мера хаоса системы. А.А. Петрушенко справедливо отмечает, что энтропия –это функция «привязанная» к поведению простых атомарно-молекулярных систем. «Энтропия проявляется в разных формах, а термодинамическая форма энтропии является лишь частным случаем» [173].

Представления о хаосе и порядке субъективны. Энтропия количественно характеризует беспорядок только простых систем. Для сложных систем еще предстоит найти способ, характеризующий порядок – беспорядок. Сложные системы многоплановые. Беспорядок в одних функциях может компенсироваться порядком в других. Ученый может быть очень упорядочен в своих умозаключениях, но   совершенно беспомощным в бытовых вопросах. Философ способен гносеологически организовать мир, но не умеет починить водопроводный кран.

Прежде чем продолжить анализ следует обратить внимание, что Больцман упростил Мир до предела, представив его идеальным газом, не учитывая того, что все молекулы гетерогенны, отличаются энергией, взаимодействуют друг с другом, находятся в поле тяжести, имеют предпочтительные состояния. Несмотря на это энтропию не критично стали привлекать для описания сложных развивающихся объектов. Еще Больцман использовал энтропию для характеристики биологических явлений и сверхсложной Вселенной. Согласно Больцману жизнь уменьшает свою энтропию, а Вселенная идет к тепловой смерти.

Антитезой Больцману выступали эволюционисты. В частности Дарвин показал, что процессы, происходящие в Мире, в ходе эволюции (возникновение жизни) не только не деградируют, но все время усложняются (понятие сложность рассматривалось выше). Первая половина 20 века вопреки прогнозу Л. Больцмана принесла человечеству модель рождения и эволюции Вселенной, где над деструктивными процессами преобладали процессы самоорганизации и агрегации вещества. В главе 8 будет показано, что вопреки Больцману главным трендом развития является агрегация вещества и переход связанной энергии в кинетическую. В разделе 2.3 приводится схема развития  агрегатов вещества.

Понятием энтропия продолжают пользоваться не только биологи. В 1948 К. Шеннон ввел понятие «энтропия» в теорию информации [232]. Если сигнал на выходе канала связи является точной копией сигнала на входе то, с точки зрения теории информации, это означает отсутствие энтропии. Формулы Больцмана (S = K ln W) и Шеннона (H = -∑Pi log₂ Pi) имеют лишь внешнее сходство. Смысл  энтропии Шеннона сводится к достоверному отличию одного сигнала от другого. Сам Шеннон предостерегал от чрезмерного расширение его энтропии и сопоставления её с термодинамической энтропией. Но произошло то, чего остерегался Шеннон.

Приведём пример, когда развитие изолированной системы, не сопровождается ростом беспорядка [236, 237]. Безусловно, состояние жидкой воды более хаотично, чем состояние кристаллической воды (льда.) Поместим смесь льда и воды в изолированную камеру. Температура льда существенно ниже температуры воды. Если льда в смеси больше, чем воды, то через некоторое время вся вода замерзнет. В термостате не окажется хаотической воды, а будет только упорядоченный лед. Получается, что в изолированной системе идет самопроизвольный процесс роста упорядоченности, а это противоречит утверждениям термодинамики. Если взять избыток жидкой воды и мало льда, то процесс пойдет в обратном направлении. Лед перейдет в жидкую воду. Итак, при некоторых условиях процесс самоорганизации в изолированной системе может быть направлен не к хаосу, а к макроскопическому порядку. Для того, чтобы окончательно избавиться от догмы, накладывающей запрет на возможность развития изолированных систем, рассмотрим ряд примеров.

Изолированная система представляет собой некоторую совокупность элементов и связей, помещённых в оболочку, непроницаемую для вещества и потоков энергии. В такой изолированной системе должны соблюдаться законы сохранения энергии и вещества. Если бы из системы «утекало» вещество, то внутри системы законы сохранения не соблюдались бы. Принято считать, что развитие в некоторой системе может протекать только с использованием ресурсов, которые находятся во внешней среде. Покажем, что это не всегда так.

Построим изолированную систему, в которую включим источники ресурсов и подсистемы утилизации «отходов». В такой изолированной системе будут протекать любые процессы, в том числе и развитие с усложнением, пока не истощаться запасы ресурсов.  Промышленные предприятия могут работать месяцами на запасенных ресурсах. Морской лайнер без дозаправки может пересечь океан. Солнце и Солнечная система, которая очень слабо связана с другими звездными системами в нашей галактике, развивается уже 5 млрд. лет. Энергия Солнца черпается из внутренних процессов синтеза «тяжелых» элементов.

Наша Вселенная развивается за счет энергии, выделившейся при Большом взрыве в начальной стадии эволюции. Если наша Вселенная изолированная, то она развивается на внутреннем источнике ресурсов. Сложившееся заблуждение о косности изолированных систем основывается на опытах, проведенных на системах очень малой энергоёмкости, где затухание процессов протекало быстро, и переходные состояния из наблюдения исключались. Незаметно лабораторные представления перенесли на макро и мега системы.

В свете изложенного материала, целесообразно обсудить утверждение, что свойствами диссипативных систем являются открытость, неравновесность и нелинейность. Это утверждение не вызывает возражения, но такие же свойства могут присутствовать и в изолированных системах. Следует добавить, что «изолированность» понятие не абсолютное. Полностью изолированных систем не бывает. Существуют системы с очень ограниченным обменом с окружением. С момента изоляции система может длительно дрейфовать к равновесному состоянию, поэтому и в изолированной системе присутствует состояние «неравновесности». Наша планета до сих пор не пришла к равновесному состоянию и продолжает миллиарды лет остывать. На глубинах 40 - 80 километров температура превышает 1000⁰ С.

Возвращаясь к энтропии, можно добавить, что все законы термодинамики носят статистический характер и «работают» только в системах, где элементами являются атомы или молекулы, причём при высокой плотности вещества. Если рассматривать очень разряженные газы, когда в 1см³ имеются единицы молекул, то в этих случаях законы термодинамики и понятие «энтропия» не приемлемы. Если молекула всего одна, то можно говорить о её внутреннем состоянии, но не о количестве возможных перестановок с другими молекулами. Следовательно, даже не все молекулярные системы можно характеризовать энтропией.

В мегамире имеются системы, содержащие сотни миллиардов кинетических единиц. Например, галактики, содержат сотни миллиардов звезд. Каждая звезда обладает кинетической энергией (движение). Звёзды связаны силами гравитации в скоплениях (галактики), которые довольно стабильно сохраняют свою форму. Однако звездные агрегаты и звезды не принято характеризовать энтропией. В процессе жизненного цикла звезда от состояния плазмы (хаос) самопроизвольно переходит к более упорядоченной нейтронной звезде. Видим стремление от хаоса к порядку, а не наоборот.

Обратимся к миру живых и социальных систем и посмотрим, есть ли там место для энтропии. Проследим, как изменяется количество элементов в единице объема при восхождении по эволюционной лестнице.

В нормальных условиях в 1 см³ газа содержится около 10¹⁹ молекул. В живой клетке плотность вещества выше, но элементами являются не атомы, а гигантские белковые молекулы. Оценим приблизительно 10¹⁴-10¹⁵ молекул в 1см³. Живые ткани содержат в 1 см³ ~ 10 ⁹ клеток. Организм имеет несколько сот органов. Чем выше иерархический уровень объекта, тем меньше кинетических  элементов содержится в единице объема. Но при малом количестве элементов энтропия «теряет свои полномочия», так как функция S= K ln W статистическая.

В научном мышлении существует мнение, что живое создает вокруг себя беспорядок (хаос), но повышает свою упорядоченность (Винер, Шредингер). Это следует понимать так. Живое потребляет высокоупорядоченные ресурсы, а сбрасывает в окружающую среду нечто мало организованное. Докажем, что это стойкое заблуждение, как и использование понятия «энтропия» для биологических объектов.

Растения потребляют из атмосферы газы (CO₂), из почвы воду и некоторые микроэлементы. В окружающую среду они отдают газы (O₂, CO₂, H₂O), некоторые метаболиты и рассеивают тепло. В первом приближении энтропия входных и выходных материальных потоков отличается мало (на входе газ и на выходе газ). Животные, потребляющие кроме газов и воды высокоорганизованную материю в виде белков, жиров, углеводов, трансформируют их в свое тело аналогичной сложности. В биосфере отходы одних организмов являются высококачественным питанием для других, поэтому ценные метаболиты организмов нельзя считать веществом с высокой энтропией.

Более того, живое вещество по Вернадскому не упрощает косную материю, а даже усложняет, множит разнообразие. Нефть, уголь, месторождения железа, бокситов, мела, известняка и многих других минералов созданы живым веществом. Поддержание неравновесного состояния кислородной атмосферы Земли является следствием деятельности живого [74]. Тогда о какой же деградации окружающей среды идет речь?

Однако наблюдается деградация энергии. «Высококачественная» световая энергия Солнца превращается в энергию химических связей тканей растений, которая затем деградирует в тепло. Однако переход света в тепло не является исключительной спецификой  живого. Этот процесс еще с большей интенсивностью осуществляется неживой материей. Поверхность Земли поглощает весь свет Солнца и в виде тепла излучает энергию обратно в космос, а живое вещество утилизирует всего несколько процентов солнечной энергии.

Оппоненты могут возразить, что человек уменьшает разнообразие биосферы и этим увеличивает ее энтропию. Действительно человек уменьшает разнообразие “дикой” биосферы, но при этом увеличивает разнообразие “культурной” биосферы (домашние животные и растения). Невероятно быстро растет разнообразие техносферы, естественно входящей в понятие внешней среды для человека. Кроме того, разнообразие системы прямо никак не связано с величиной энтропии. Принято считать, что кристаллический порядок содержит минимумом энтропии, но трудно придумать что - либо  более однообразное, чем кристалл. Наиболее развитые предприятия и организации общества стремятся упростить систему управления, но это никак нельзя связывать с деградацией. Более того, разнообразие биосферы изменялось многократно без вмешательства человека. Палеонтология отмечает массовые вымирания в океанах на протяжении 600 млн. лет [202].

Нельзя понять сложное явление, опираясь на очень простые модели. Попытайтесь описать архитектуру здания, зная только структуру кирпича. Хотя законы термодинамики способны описать газ, но для характеристики дома их явно не достаточно.

Можно показать, что в сложных системах законы термодинамики не нарушаются. Они там просто не действуют. Законы термодинамики действуют в идеализированных системах, где из триединого ВЭИ во внимание принимается только тепловая энергия. Не включаются в функции термодинамической системы другие стороны объектов (вещество, информация, структура, саморазвитие, управление, форма, цвет, запах эмоции, сознание и пр.). Термодинамика «слепа» ко многим сторонам мира. В сложных объектах, которые являются совокупностью множества различных систем, энтропия «работает» на уровне молекулярных агрегатов. В качестве метафоры можно привести образ дома.

Допустим, нижний этаж состоит из молекул. Рост «энтропии» фундамента (выравнивание температуры, гомогенизация состава бетона, рассасывание внутренних напряжений) только укрепляет фундамент и не влияет на состояние крыши и настроение жильцов верхних этажей. 

Несмотря на сказанное, понятием «энтропия» оперируют в разных науках, следовательно, в этом есть некоторая потребность. Попытаемся её понять.

В молекулярных системах в ряду газ - жидкость – кристалл энтропия уменьшается. Визуально в этом ряду возрастает и способность сохранять структуру (форму). Газ стремится неограниченно расшириться и не имеет формы. Капля жидкости уже оформлена (сфера), но ещё не прочно. Кристалл представляет образец устойчивости. Живое вещество существует и сохраняет устойчивость, упорядоченность, но не вследствие понижения энтропии, а благодаря агрегированию и процессам управления. По своей сути и энтропия Шеннона, характеризуя устойчивость сигнала к помехам, является мерой неустойчивости, мерой «зашумленности» канала связи. Итак, в случае с энтропией произошла подмена понятий, под энтропией стали понимать меру устойчивости системы.

 

5.3. Устойчивость и флюктуации

Факт, но ничего вечного во Вселенной нет. Рано или поздно даже самый устойчивый объект неизбежно переходит в другое состояние. Каждая организованность имеет свой средний срок существования. Молекулы водяного пара (Т>100⁰C) сталкиваются, образуют кластеры, которые тут же распадаются, возникают вновь и опять распадаются. Время жизни таких кластеров составляют менее 10^-9с. [194]. В жидкой воде кластеры существуют дольше, чем в газе. Лед может существовать десятки тысяч лет, если Т<0⁰C.

На фоне устойчивого процесса всегда наблюдаются флюктуации - апериодические отклонения параметров организации от некоторой средней величины. При моделировании организации часто на флюктуации внимания не обращают, используя усреднённые характеристики. Это может привести к анекдотическим заключениям типа «у пациентов больницы средняя температура находится в норме».

В главе 3 мы ввели понятие стохастический каркас псевдо сейф – систем. Стохастические связи порождают флюктуации. Одни связи разрушаются, а другие возникают, в среднем всё идёт нормально. Усреднения маскируют многие тонкие процессы самоорганизации, выводят их из поля исследования. Если сравнить размер звезды (10¹⁰см.) и размер нашей Вселенной ~ (10²⁸см.), то взрыв отдельной звезды – это ничтожная флюктуация. Однако взрыв звезды для её планет и возможной жизни на них «не пустяк».

Все законы термодинамики носят статистический, усреднённый характер. Например, второй закон термодинамики утверждает, что тепло не может передаваться от холодного тела к горячему, но это только в среднем. Если рассматривать передачу энергии на уровне одной молекулы, то второй закон термодинамики уже неприменим.

                        1

 

                             2                             V₂

 

                                                                V₃

V₁

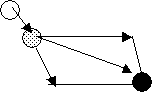
Рис. 5.3. Схема перераспределения энергии между молекулами.

 

В «холодном» теле всегда есть определенная доля «горячих» молекул, которые могут передавать свою энергию к более нагретому телу (по средней температуре). На рис. 5.3 представлена схема такого события:

Пусть молекула 1 со скоростью V₁ сталкивается с молекулой 2, движущейся со скоростью V₂. В результате молекула 2 изменит траекторию своего движения, и будет двигаться с большей скоростью V₃. Таким образом, энергия от «холодной» молекулы 1 передалась «горячей» молекуле 2. Для мифических существ, живущих на молекуле, усредненный закон о невозможности такого события будет слабым утешением.

Второй закон термодинамики «запрещает» вечный двигатель с такой категоричностью, что заявки на изобретение вечного двигателя не принимаются к рассмотрению. «Вечный» означает, что без притока энергии извне он долго не работает. Поскольку мы постулировали, что изолированных систем в природе не существует, то постановка вопроса о вечном, изолированном двигателе не имеет смысла. Через каждый «двигатель» должен протекать поток ВЭИ. Неясно, как долго должен работать двигатель, чтобы считаться «вечным»? Солнце работает на внутренней энергии миллиарды лет, Вселенная – десятки млрд. лет. Если Вселенная является изолированной системой, то мы имеем прецедент вечного движения. Очевидно, законы термодинамики, как и все другие «законы», имеют ограниченную область применения.

 

                                                                  

 

 

 

 

 

 

 

 

 

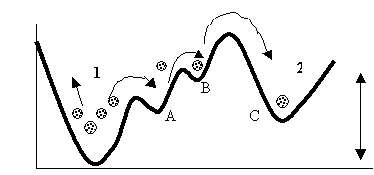
Рис. 5.4. Механическая модель флюктуационного двигателя эволюции.

 

Можно показать, как нелюбимые термодинамикой флюктуации, исполняющие роль организаторов развития, являются двигателями эволюции (рис.5.4).

В ямке 1 находится множество шариков. Имитация флюктуаций осуществляется хаотической вибрацией всей системы «вверх-вниз». Амплитуды вибрации не достаточно, чтобы сразу перебросить шарик в ямку 2. Перескок влево требует большей энергии, чем вправо, что детерминирует движение вправо. Однако в ходе хаотических столкновений шаров и флюктуаций энергии иногда некоторый шар может достигнуть впадины А, где задержится на какое-то время. Сама впадина А может быть следствием некоторой флюктуации пространства. Она может появляться и исчезать. Если она появилась в нужный момент, когда шарик до нее долетел, то впадина сыграет роль трамплина. После этого она может исчезнуть. От вибрации шарик может вернуться обратно в ямку 1, что более вероятно, но иногда может перескочить в ямку В (менее вероятно). Точно также он может достигнуть устойчивого положения С. При достаточно большой длительности эксперимента какой-то из шаров сумеет по флюктуационной «лестнице эволюции» достигнуть более высокого уровня. Попав в ямку 2, шар приобретает устойчивое состояние и обратно вернуться не сможет, если не усилить амплитуду вибрации.

Итак, что невозможно было сделать в одно движение, удалось осуществить в результате хаотических множественных столкновений шаров и случайных ступенек. Для реализации эволюционного скачка потребовалась асимметрия системы и наличие нескольких переходных, неустойчивых промежуточных состояний. Итак, для направленной эволюции необходимы: асимметрия сил (связей), источники энергии и множество попыток. Предсказать такое развитие событий классическая термодинамика не способна, т.к. оперирует только среднестатистическими значениями.

В неживых системах устойчивость (длительное существование) достижима при условии минимизации энергии системы, т.е. нахождения объекта в некоторой потенциальной энергетической «яме». «Яма» является препятствием для внешних дестабилизирующих воздействий. Кроме минимума внутренней энергии важно, чтобы диссипация энергии была минимальной («экономная система»). В живых системах изобретен другой, динамический способ поддержания устойчивого неравновесия (рис. 5.5).

					В

 

 

 

 

 

 

 

 

 

 

 

 

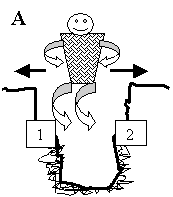
Рис.5.5. Принцип динамической устойчивости.

 

Допустим, человек находится на ступеньке 1, куда невозможно поставить две ноги и удерживать равновесие. На другой стороне ямы есть такая же ступенька 2. Избежать падения можно только в том случае, если человек будет непрерывно перепрыгивать со ступени 1 на ступень 2 и обратно. Такой способ избегания падения требует источника энергии и средств обработки информации (ритм прыжков). Именно таким способом живые системы, не дожидаясь смерти, воспроизводят потомство, сохраняют свой гомеостазис.

Таких примеров саморегуляции живых и кибернетических систем очень много. Велосипедист удерживает равновесие благодаря непрерывному падению. Ракета находит цель благодаря непрерывному «рысканию» (отклонению от курса) и т.д. Способы стабилизации хорошо изучены в кибернетике и основаны на обратных связях [46].

Пример рис. 5.5А иллюстрирует стабилизацию (гомеостазис) системы, работают отрицательные обратные связи. Рис 5.5 В моделирует изменчивость (гомеокинез), скачки по лестнице усложнения.

Для эволюции должно существовать некоторое однонаправленное «поле сил». Эволюция жизни на Земле происходила на фоне однонаправленного уменьшения температуры, уменьшения радиоактивности, повышения активности Солнца и т.п. Любое движение обуславливается неравновесием сил.

В главе 3 рассмотрен принцип гетерархии организаций, асимметричности связей. Для всех организаций (не только живых) коридор развития задаётся «системной памятью» [57]. Прыгающий мячик всегда будет стремиться скатиться с горы, но не забраться на вершину. В данном случае склон горы является системной памятью о прошлых процессах горообразования.

Возвращаясь к рис. 5.4 целесообразно вспомнить известный в квантовой физике туннельный эффект, заключающийся в том, что элементарная частица, например электрон, может быть обнаружена в зоне 2, хотя энергии для перехода из положения 1 в положение 2 теоретически ей не хватает. Квантовая физика [31, 124] не дает объяснения причин «туннельного» эффекта. Пример рисунка 5.4 дает возможность объяснить туннельный эффект не только в микромире, но и в макромире, при этом не прибегая к представлениям квантовой физики. Объект попадает в зону 2 на «волне» флюктуаций.

Есть еще одно свойство флюктуаций, которое появилась в свете нашей трактовки понятия информации. Флюктуации - это разновидность неоднородностей, т.е. разновидность информации. Одна информация порождает другую.

 

Выводы

1.       Умопостигаемое количество информации оценивается как порядок.

2.       Непознанный порядок считают хаосом. Появление познаваемых структур оценивается как упорядочение.

3.       Энтропия (мера хаоса) ограничена в применимости, т.к. из триединства вещества, энергии, информации описывает только энергетическую составляющую тепловых процессов.

4.       Энтропия не может служить  мерой беспорядка в сложных системах.

5.        В популярном изложении устойчивость систем разной сложности подменили понятием «энтропия».

6.       Вопреки росту энтропии Мир развивается от сложного порядка к более простым агрегатам.

7.       Статистические законы термодинамики маскируют процессы самоорганизации Мира.

8.       Самоорганизация, направленная эволюция происходит на уровне флюктуаций. Для этого необходима асимметрия сил, источники энергии и множество попыток.

 

Copyright© 2007  Попов В.П.  Организация. Тектология XXI. All Rights reserved